
役職:准教授
居室:25-621A
email:matsuura(at)ae.keio.ac.jp
教員プロフィール:
https://www.st.keio.ac.jp/tprofile/ae/matsuura.html
研究者情報データベース:
https://k-ris.keio.ac.jp/html/100011502_ja.html
統計学、多変量解析、統計的品質管理
多変量解析や品質管理における統計学的手法の開発を中心に統計学の理論と応用に関する研究を行っています。具体的な研究テーマとしては、(1) 多変量重回帰分析、(2) 分布のprincipal points(主要点)、(3) 応答曲面法、などにおける統計的推定問題が挙げられます。
管理工学輪講、卒業研究、理工学基礎実験、管理工学実験・演習5、管理工学基礎演習Ⅱ、管理工学概論
統計解析、多変量解析第1、開放環境科学課題研究、開放環境科学特別研究第1、オープンシステムマネジメント同演習
興味がある変数(目的変数)yを、その変数に関連があると考えられる変数(説明変数)xを用いて、なるべくデータにうまく当てはまるような近似式 y=f(x) を求めることを回帰分析と言います。下の図(左)では、ある商品の1日の売上個数yを、その日の最高気温xの1次式 y=ax+b で当てはめようとしています。説明変数は一つとは限らず複数ある場合もあり(例えば、最高気温以外にもその商品の売り上げに影響する要因があるかもしれません)、その場合を重回帰分析と言います。さらに目的変数も複数の場合があり(例えば、商品は1種類ではないかもしれません)、これをしばしば多変量重回帰分析と言います。複数の変数を扱うことで、詳細な分析が可能になり、より有益な情報がデータから引き出せる可能性がありますが、モデルが複雑になる分、適切な定式化、適切なデータ解析が必要です。そのためには、統計学・数学の知識が不可欠です。当研究室では、多変量重回帰分析に関して、より高精度な統計解析手法を導くことに取り組んでいます。
データの「平均値」というのは、データの全ての和をデータ数で割ったものであり、そのデータの分布を代表的な1つの値に縮約したものになります。これに対し、principal points(主要点)というのは、分布を代表的な複数の値で縮約したものになり、「平均値」の概念を複数個に拡張したものと見ることができます。当研究室では、このprincipal pointsについて、特に多変量分布の場合を中心に、その挙動や、データからのprincipal pointsの推定問題などに取り組んでいます。
品質管理や製品設計などで、興味のある特性について、その特性に影響する(複数の)因子の値を実験計画に従って設定して、決められた数の実験を行い、実験結果を基に特性と因子の間に主に2次曲面の関係式(応答曲面式)を導くことを応答曲面法と呼びます。当研究室では、この応答曲面法に関連する統計学的な研究課題、例えば応答曲面式の推定精度や、影響の大きい因子の適切な選択法(変数選択法)などに取り組んでいます。
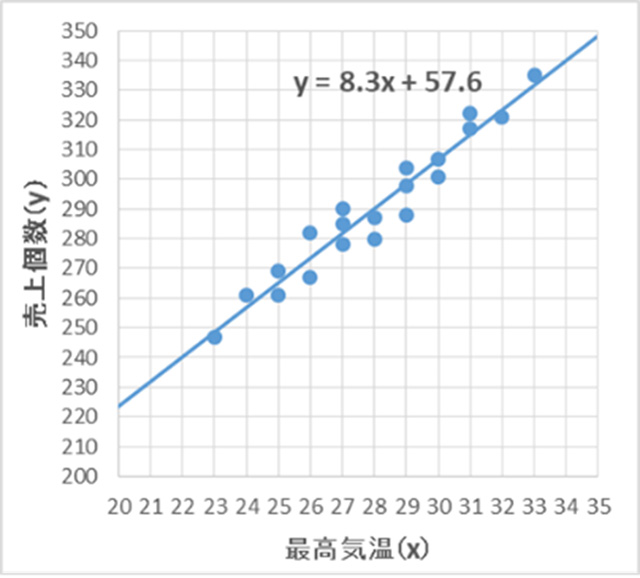
回帰分析
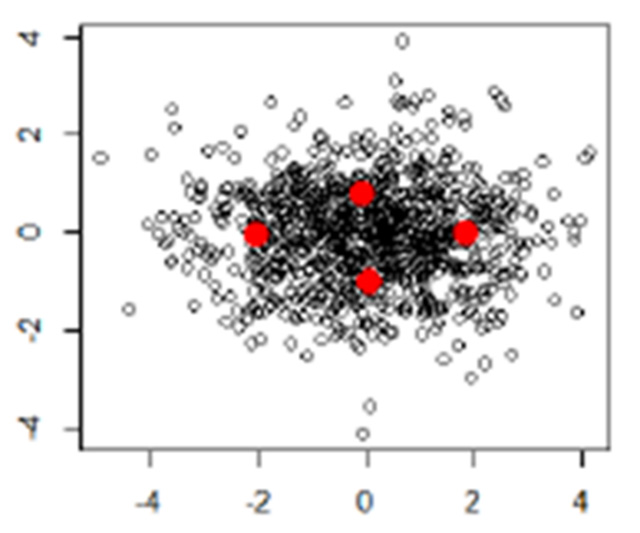
principal points
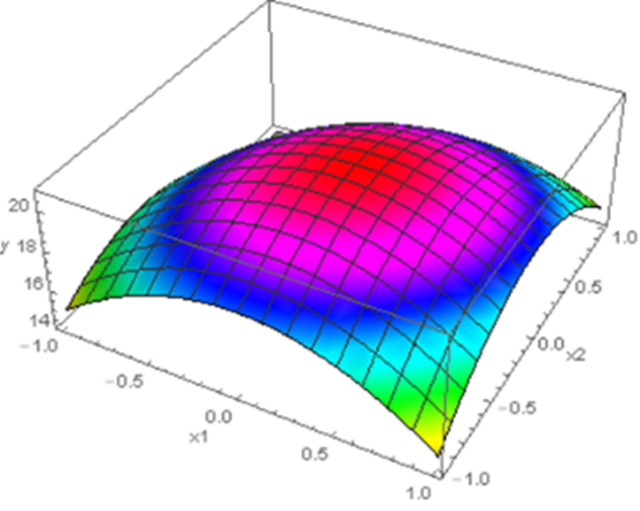
principal points
近年、多種多様なデータに対する様々なデータ解析手法が開発され、発展を遂げてきています。これらのデータ解析手法を学ぶことはもちろん重要ですが、一方で、各データ解析手法が、どのようなモデルの想定の下、どのような基準の下に解析手順が構成され、どのような精度を持つのか、ということに対して、自分の力で吟味することができるようになることも大切であると考えています。そのために、統計学、多変量解析の理論的基礎をしっかり学び、各データ解析手法の統計学・数学的バックグラウンドをきちんと理解し、活用できる学生を社会に送り出したいと考えています。