成島研究室narushima Lab.

研究の概要

オペレーションズ・リサーチ、中でも数理最適化に関する研究を行っています。数理最適化問題は、工学や社会科学など様々な分野で発生する問題ですが、情報技術の発展や社会の複雑化により、問題も複雑化・大規模化してきています。そのような問題に対するモデル化とモデル化した問題を実際に解くためのアルゴリズムの開発、という両面で研究しています。

担当講義科目

管理工学実験・演習４、管理工学基礎演習Ⅰ、理工学基礎実験、管理工学用数学第1、オペレーションズ・リサーチ第2、オペレーションズ・リサーチ第4、人間とシステム

①大規模な最適化問題に対する研究

近年の高度情報化社会の流れから、扱うデータ量が増えてきています。そのため、近年では、いわゆる大規模な最適化問題が増えてきています。しかしながら、大規模な最適化問題は必ずしも既存の方法で解決できるとは限りません。そのため、大規模な最適化問題に対するモデル化や解くためのアルゴリズムに関する研究を行っています。

• 

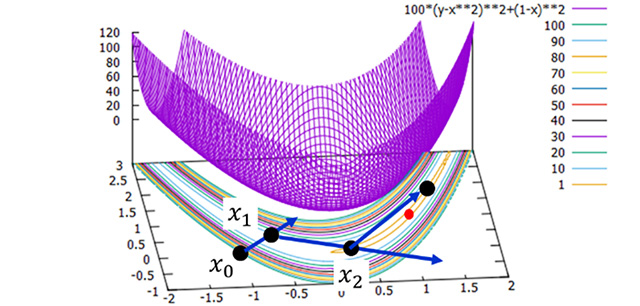
  図1：数理最適化のイメージ

②ロバストな最適化問題に対する研究

例えば、複数の製品の生産量を決定することによって販売利益を最大にしようという最適化問題があったとします。その場合、製品の単位利益などは一定の値としてモデル化されますが、実際には外部要因（例えばガソリン価格の高騰による輸送費の変動など）によって変化することが一般的です。このように、不確実な状況を含むような最適化問題に対して頑健（ロバスト）な最適解を与えるような方法の研究を行っています。

③均衡問題に対する研究

通常、意思決定者が一人の場合には数理最適化問題となりますが、複数の意思決定者がいて、お互いに影響を及ぼすような、いわゆる競合が生じるような場合に生じる問題は、均衡問題と呼ばれ、通常の最適化問題より複雑な問題となります。そのため、均衡問題に対するモデル化や均衡問題を解くためのアルゴリズムについて研究を行っています。

近年の研究テーマ

• 機械学習などで生じる超大規模な最適化問題に対するアルゴリズムの構築
• サプライチェインネットワークで生じる均衡問題に対する研究
• 分散投資問題に対するロバストなポートフォリオの構築

教育目標・方針

数理最適化では、実際に社会で生じる問題に対するモデル化とそれを解くためのアルゴリズムがそろって初めて問題が解決できます。しかしながら、近年の最適化問題の大規模化・複雑化に伴って、問題を解くためのアルゴリズムの整備も必要不可欠となっています。当研究室では、モデル化とアルゴリズムの両面の知識を持ち、実際の問題に対して、高い問題解決力を有する人材を育成することを目標としています。